一、蒙日圆与双切线问题:
圆锥曲线的正交切线交点轨迹
在椭圆中,任意两条互相垂直的切线的交点都在同一个圆上,它的圆心是椭圆中心,半径等于长、短半轴平方和的算术平均根,这个圆就是蒙日(Monge)圆,也叫外准圆。
$(1)椭圆\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1的正交切线交点轨迹为x^2+y^2=a^2+b^2;$
$(2)双曲线\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1的正交切线交点轨迹为x^2+y^2=a^2-b^2;$
$(3)抛物线y^2=2px的正交切线交点轨迹为准线方程x=-\cfrac{p}{2};$
以上反之也成立。
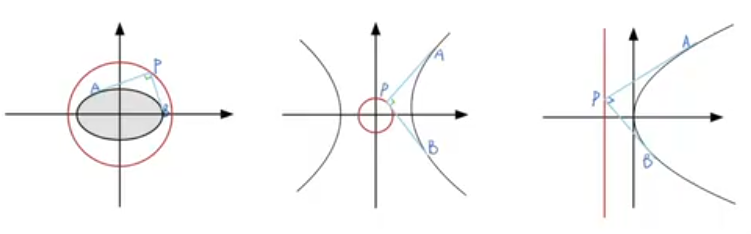
$设P({\color{Red}x_0,y_0}),A(x_1,y_1),B(x_2,y_2)$
$设PA:y=k_1(x-x_0)+y_0;\qquad PB:PA:y=k_2(x-x_0)+y_0;\quad k_1k_2=-1$
$\begin{cases} y=k_1(x-x_0)+y_0\\ \quad \\ \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\end{cases}\Rightarrow \begin{cases} y=k_1x+{\color{Red} (y_0-k_1x_0)}\\ \quad \\ \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\end{cases}$
$\Rightarrow b^2x^2+a^2y^2-a^2b^2=0\Rightarrow b^2x^2+a^2[k_1(x-x_0)+y_0]^2-a^2b^2=0$
$\Rightarrow b^2x^2+a^2[k_1x+{\color{Red} (y_0-k_1x_0)} ]^2-a^2b^2=0$
$\Rightarrow b^2x^2+a^2[k_1^2x^2+2k_1{\color{Red} (y_0-k_1x_0)} x+{\color{Red} (y_0-k_1x_0)} ^2]-a^2b^2=0$
$\Rightarrow(a^2k_1^2+b^2)x^2+2k_1a^2{\color{Red} (y_0-k_1x_0)} x+a^2{\color{Red} (y_0-k_1x_0)} ^2-a^2b^2=0$
$相切,所以{\color{Red}\Delta-0}$
$\because \Delta =4k_1^2a^4(y_0-kx_0)^2-4a^2(a^2k_1^2+b^2)[(y_0-k_1x_0)^2-b^2]=0$
$\Rightarrow k_1^2a^2(y_0-kx_0)^2=(a^2k_1^2+b^2)[(y_0-k_1x_0)^2-b^2]$
$\Rightarrow k_1^2a^2(y_0-kx_0)^2=a^2k_1^2(y_0-k_1x_0)^2-a^2b^2k_1^2+b^2(y_0-k_1x_0)^2-b^4$
$\Rightarrow a^2b^2k_1^2+b^4=b^2(y_0-k_1x_0)^2$
$\Rightarrow a^2k_1^2+b^2=(y_0-k_1x_0)^2$
同理,联立 $\begin{cases} y=k_2(x-x_0)+y_0\\ \quad \\ \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\end{cases}\Rightarrow \bigtriangleup =0$解得$\Rightarrow a^2k_2^2+b^2=(y_0-k_2x_0)^2$
$显然k_1,k_2是关于k的一元二次方程a^2k^2+b^2=(y_0-kx_0)^2的两个根$
$a^2k^2+b^2=(y_0-kx_0)^2\Rightarrow (a^2-x_0^2)k^2+2x_0y_0k+b^2-y_0^2$
$\Rightarrow {\color{Red} k_1k_2=\cfrac{b^2-y_0^2}{a^2-x_0^2} =-1}\Rightarrow {\color{Red} b^2-y_0^2+a^2-x_0^2 =0 \Rightarrow x_0^2+y_0^2=a^2+b^2}$
$题目1、c在平面直角坐标系XOY中,已知圆O:x^2+y^2=25,圆C:x^2+(y-1)^2=r^2(0\lt r \lt 3),点P(-3,4),$
$M,N为圆O上异于点P的两点,若直线PM,PN与圆C都相切。$
$求证:当r变化时,直线MN的斜率为定值。$
$设M(x_1,y_1),N(x_2,y_2),P(-3,4)PM:y=k_1(x+3)+4,PN:y=k_2(x+3)+4$
$PM与x^2+(y-1)^2=r^2相切, 则有:$
$\cfrac{\left | 3k_1+3 \right | }{\sqrt{1+k_1^2} }=r{\color{Red} \quad直线与圆相切用圆心到直线的距离=r;直线与椭圆相切用\Delta=0} $
$\Rightarrow 9(k_1+1)^2=r^2(1+k_1^2)$
$同理,PN与x^2+(y-1)^2=r^2相切,则有:\Rightarrow 9(k_2+1)^2=r^2(1+k_2^2)$
$故k_1,k_2是关于k的一元二次方程\Rightarrow 9(k+1)^2=r^2(1+k^2)的两个根$
$得:(9-r^2)k^2+18k+9-r^2=0$
$k_1k_2=1\Rightarrow {\color{Red} \cfrac{y_1-4}{x_1+3} \cfrac{y_2-4}{x_2+3} =1\Rightarrow y_1y_2-4(y_1+y_2)+16=x_1x_2+3(x_1+x_2)+9}$
$设MN :y=kx+m与圆O联立,\begin{cases}y=kx+m \\\quad\\x^2+y^2=25 \end{cases}$
$\Rightarrow (1+k^2)x^2+2kmx+m^2-25=0,$
$x_1+x_2=\cfrac{-2km}{1+k^2};\qquad x_1x_2=\cfrac{m^2-25}{1+k^2}$
$y_1+y_2=kx_1+m+kx_2+m=\cfrac{-2k^2m}{1+k^2}+2m=\cfrac{2m}{1+k^2}$
$y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=\cfrac{k^2(m^2-25)}{1+k^2}+\cfrac{-2k^2m^2}{1+k^2}+m^2$
$=\cfrac{k^2m^2-25k^2-2k^2m^2+k^2m^2+m^2}{1+k^2}=\cfrac{m^2-25k^2}{1+k^2}$
$代入上式得:\cfrac{m^2-25k^2}{1+k^2} -4\cfrac{2m}{1+k^2}+16=3\cfrac{-2km}{1+k^2}+\cfrac{m^2-25}{1+k^2}+9$
$\Rightarrow m^2-25k^2-8m+7(1+k^2)=-6km+m^2-25\Rightarrow 9k^2-3km+4(m-4)=0$
$(3k-4)[3k-(m-4)]=0,解得k=\cfrac{4}{3},k=\cfrac{m-4}{3}$
$若k=\cfrac{m-4}{3},代入y=kx+m,得直线MN过(-3,4),舍去,故直线MN的斜率为定值\cfrac{4}{3}$
$题目2、2018年浙江高考,已知点P是y轴左侧(不含y轴)一点,抛物线C:y^2=4x上存在不同的两点A,B$
$满足PA,PB的中点均在C上。$
$(1)设AB中点为M,证明:PM垂直于y轴。$
$(2)若点P为半椭圆x^2+\cfrac{y^2}{4}=1(x\le 0)上的动点,求\triangle PAB面积的取值范围。$
$分析:设P(x_0,y_0),A(x_1,y_1),B(x_2,y_2),证2y_0=y_1+y_2即可$
$这里设AB的横坐标为x_1,x_2令问题变得得很复杂,不如直接利用AB在抛物线上这个约束条件。$
$即x_1=\cfrac{y_1^2}{4} ,x_2=\cfrac{y_2^2}{4}{\color{Red} \qquad点在抛物线上,只设一个坐标} $
$解:设P(x_0,y_0),A(\cfrac{y_1^2}{4},y_1),B(\cfrac{y_2^2}{4},y_2)$
$则PA的中点坐标(\cfrac{y_1^2}{8}+\cfrac{x_0}{2},\cfrac{y_1+y_0}{2})代入y^2=4x$
$\Rightarrow (\cfrac{y_0+y_1}{2})^2=4\cdot (\cfrac{y_1^2}{8} +\cfrac{x_0}{2} )\Rightarrow$
$y_{\color{Red} 1} ^2-2y_0y_{\color{Red} 1} +8x_0-y_0^2=0$
$同理PB中点可得:y_{\color{Red} 2} ^2-2y_0y_{\color{Red} 2} +8x_0-y_0^2=0$
$由此可见y_1,y_2是关于 y的方程{\color{Red} y} ^2-2y_0{\color{Red} y} +8x_0-y_0^2=0的两根。$
$y_1+y_2=2y_0,得证$
练习:
1、 已知圆O:$x^2+y^2=1$,若直线$y=kx+2$上总存在点P,使得过点P作圆O的两条切线相互垂直,则实数$k$的取值范围是:
由蒙日圆概念可知,P点的轨迹为$x^2+y^2=2$,由于P点又在直线$y=kx+2$上,即点P既在圆上又在直线上,也就是说直线与圆恒有公共点,即直线与圆相切或相交。依据点到直线的距离,可知圆心O到直线的距离$d\le r\Rightarrow \cfrac{2}{\sqrt{1+k^2}}\le \sqrt{2}\Rightarrow 1+k^2\ge 2 \Rightarrow k\ge 1或k\le -1$
另证P点轨迹为圆的过程:
$设P(x_0,y_0),切线PA的方程为:y-y_0=k_1(x-x_0) \Rightarrow y=k_1x+y_0-kx_0,$
$圆心(0,0)到直线的距离为1,\Rightarrow \cfrac{|y_0-k_1x_0|}{\sqrt{1+k_1^2} } =1\Rightarrow 1+k_1^2=(y_0-k_1x_0)^2$
$\Rightarrow (x_0^2-1)k_1^2-2x_0xy_0k_1+y_0^2-1=0$
$同理另一条切线也可得到(x_0^2-1)k_2^2-2x_0xy_0k_2+y_0^2-1=0$
$斜率是k_1,k_2关于k的方程(x_0^2-1)k^2-2x_0xy_0k+y_0^2-1=0的两个根,故k_1k_2=\cfrac{y_0^2-1}{x_0^2-1}=-1$
2、 给定椭圆C:$\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)$,称圆心在原点O半径为$\sqrt{a^2+b^2}$的圆是椭圆C的准圆,若椭圆C的一个焦点为$F(\sqrt{2},0)$,其短轴上的一个端点到F的距离为$\sqrt{3}$.
(1)求椭圆C的方程和其准圆方程。$\quad\cfrac{x^2}{3}+y^2=1,x^2+y^2=4$
(2)点P是椭圆C的准圆上的动点,过点P作椭圆的切线$l_1,l_2$交准圆于点MN;
$①当点P为准圆与y轨正半轴的交点时,求直线l_1,l_2的方程并证明l_1\bot l_2;$
$②求证线段MN的长为定值。$
$解:①当直线l_1,l_2中有一条斜率不存在时,不妨设l_1$不存在斜率,$l_1:x=\pm \sqrt{3},当l_1:x=\sqrt{3}时,l_1$与准圆交于点$(\sqrt{3},1)(\sqrt{3},-1)$,此时$l_2$为$y=1(或y=-1)$,显然$l_1与l_24垂直,同理可证l_1:x=-\sqrt{3},直线l_1,l_2$垂直。
$②当直线l_1,l_2中有一条斜率存在时,设P(x_0,y_0),其中x_0^2+y_0^2=4$
$设经过点P(x_0,y_0)与椭圆相切的直线为y=k(x-x_0)+y_0$
$\begin{cases}x^2+3y^2-3=0\\y=k(x-x_0)+y_0\end{cases}\Rightarrow x^2+3(kx+y_0-kx_0)^2-3=0$
$\Rightarrow (1+3k^2)x^2+6k(y_0-kx_0)x+3(y_0-kx_0)^2-3=0$
$\Rightarrow \Delta =[6k(y_0-kx_0)]^2-4(1+3k^2)\cdot [3(y_0-kx_0)^2-3]=0$
$\Rightarrow 3k^2(y_0-kx_0)^2=(1+3k^2)\cdot [(y_0-kx_0)^2-1]\Rightarrow $
$3k^2(y_0-kx_0)^2=(y_0-kx_0)^2-1+3k^2(y_0-kx_0)^2-3k^2$
$\Rightarrow (y_0-kx_0)^2-1-3k^2=0整理为{\color{Red} 以k为主元}的代数式$
$(3-x_0^2)k^2+2x_0y_0k+1-y_0^2=0$
$设直线l_1,l_2的斜率k_1,k_2,因为l_1,l_2$与椭圆相切,所以$k_1,k_2$是满足方程$(3-x_0^2)k^2+2x_0y_0k+1-y_0^2=0$
$\Rightarrow k_1k_2=\cfrac{1-y_0^2}{3-x_0^2}=\cfrac{1+x_0^2-4}{3-x_0^2}=-1\Rightarrow l_1\perp l_2$
$MN是准圆的直径,所以|MN|=4$
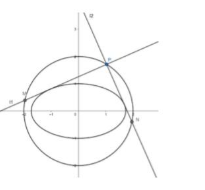
3、 2020年杭州学军中学高三月考已知抛物线$C_1:y^2=2px(p\gt 0).圆C_2:(x-1)^2+y^2=r^2(r\gt 0)$,抛物线$C_1上的点到其准线的距离的最小值为\cfrac{1}{4}.$
(1)求抛物线$C_1$的方程和其准线方程。
(2)点$P(2,y_0)是抛物线C_1$在第一象限内一点,过点P作圆$C_2$的两条切线分别交抛物线$C_1$于$A,B(A,B异于点P),问是否存在圆C_2使AB$恰为其切线,若存在,求出r值;若不存在,说明理由。
$解:①由抛物线C_1上的点到其准线的距离的最小值为\cfrac{1}{4}.\Rightarrow \cfrac{p}{2}=\cfrac{1}{4}\Rightarrow p=\cfrac{1}{2},y^2=x,准线x=-\cfrac{1}{4}$
$②由①可得P(2,\sqrt{2}),假设存在C_2使得AB恰为其切线,设A(y_1^2,y_1)B(y_2^2,y_2),则经过PA的直线方程为:$
$y-\sqrt{2}=\cfrac{y_1-\sqrt{2}}{y_1^2-2}(x-2),即x-(y_1+\sqrt{2})y+\sqrt{2}y_1=0$
${\color{Red} 抛物线可以用两点式写出直线方程,区别于椭圆和双曲线要设方程}$
$由C_2(1,0)到PA的距离为r,得\cfrac{|1+\sqrt{2}y_1|}{\sqrt{1+(y_1+\sqrt{2})^2}}=r\Rightarrow r^2[1+(y_1+\sqrt{2})^2]=(1+\sqrt{2}y_1)^2$
$化简,得(2-r^2)y_1^2+2\sqrt{2}(1-r^2)y_1+1-3r^2=0$
$同理,得(2-r^2)y_2^2+2\sqrt{2}(1-r^2)y_2+1-3r^2=0$
$所以,y_1,y_2是方程(2-r^2)y^2+2\sqrt{2}(1-r^2)y+1-3r^2=0的两个不相等实根$
$故有y_1+y_2=-\cfrac{2\sqrt{2}(1-r^2)}{2-r^2}\qquad y_1y_2=\cfrac{1-3r^2}{2-r^2}$
$故l_{AB}:y-y_1=\cfrac{y_1-y_2}{y_1^2-y_2^2}(x-y_1^2)\Rightarrow (y-y_1)(y_1+y_2)=x-y_1^2\Rightarrow x-(y_1+y_2)y+y_1y_2=0$
$由C_2(1,0)到l_{AB}的距离为r,得r=\cfrac{|1+y_1y_2|}{\sqrt{1+(y_1+y_2)^2}}所以(1+\cfrac{1-3r^2}{2-r^2})^2=r^2+r^2[-\cfrac{2\sqrt{2}(1-r^2)^2}{2-r^2}]$
$(3-4r^2)^2=r^2(2-r^2)^2+8r^2(1-r^2)^2,化简,得r^6-4r^4+4r^2-1=0,即(r^2-1)(r^4-4r^2+1)=0$
$经分析知0\lt r\lt 1,因此r=\cfrac{\sqrt{5}-1}{2}$
$解题思路分析:设点(只设纵坐标), 圆心C_2到切线PA(含y_1和r),PB(含y_2和r),同构利用韦达定理,得到y_1与y_2与r的关系,$
$圆心C_2到切线AB(含y_1+y_2,y_1y_2和r)的距离为半径,得到的式子只含y_1+y_2,y_1y_2和r$
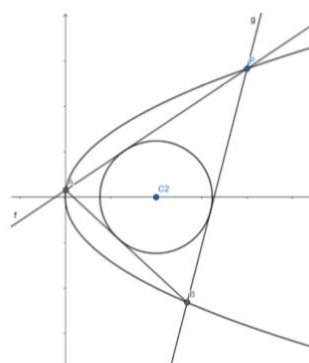
4、2019年天津二模.椭圆C:$\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)$的离心率为$\cfrac{\sqrt{3}}{2}$,直线y=1与椭圆C两交点距离为8.
①求椭圆C的方程。
②设$R(x_0,y_0)$是椭圆C上支点,由原点O向圆$(x-x_0)^2+(y-y_0)^2=4$引两条切线,分别交椭圆C于点P,Q,若OP,OQ的斜率存在,并分别记为$k_1,k_2$,求证:$k_1k_2$为定值。
③在(2)条件下,试问$\left | OP \right | ^2+\left | OQ\right | ^2$是否为定值?若是,求之,若不是,请说明理由。
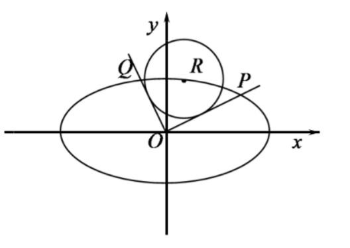
解:$①\cfrac{x^2}{20}+\cfrac{y^2}{5}=1$
$②设OP、OQ的直线方程分别为y=k_1x,y_2=k_2x,由直线OP为圆R的切线,有\cfrac{|k_1x_0-y_0|}{\sqrt{1+k_1^2}}=2$
$\Rightarrow (x_0^2-4)k_1^2-2x_0y_0k_1+(y_0^2-4)=0$
$同理可得 (x_0^2-4)k_2^2-2x_0y_0k_2+(y_0^2-4)=0$
$\therefore k_1,k_2是关于k的方程 (x_0^2-4)k^2-2x_0y_0k+(y_0^2-4)=0的两个不相等实数根$
$x^2-4\ne 0,\Delta \gt 0,则k_1k_2=\cfrac{y_0^2-4}{x_0^2-4}由R(x_0,y_0)在椭圆上,即y_0^2=5-\cfrac{1}{4}x_0^2$
$\therefore k_1k_2=\cfrac{y_0^2-4}{x_0^2-4}=\cfrac{1-\cfrac{1}{4}x_0^2}{x_0^2-4}=-\cfrac{1}{4}$
$③设P(x_1,y_1),Q(x_2,y_2)\begin{cases}y=k_1x\\ \cfrac{x^2}{25}+\cfrac{y^2}{5}\end{cases}\Rightarrow \begin{cases}x_1^2=\cfrac{20}{1+4k_1^2}\\y_1^2=\cfrac{20k_1^2}{1+4k_1^2}\end{cases}\Rightarrow x_1^2+y_1^2=\cfrac{20(1+k_1^2)}{1+4k_1^2}$
$同理,得x_2^2+y_2^2=\cfrac{20(1+k_2^2)}{1+4k_2^2},由k_1k_2=-\cfrac{1}{4}$
$\left | OP \right | ^2+\left | OQ\right | ^2=x_1^2+y_1^2+x_2^2+y_2^2=\cfrac{20(1+k_1^2)}{1+4k_1^2}+\cfrac{20(1+k_2^2)}{1+4k_2^2}=\cfrac{20(1+k_1^2)}{1+4k_1^2}+\cfrac{20(1+\cfrac{1}{16k_1^2})}{1+\cfrac{1}{4k_2^2}}$
$=\cfrac{20(1+k_1^2)}{1+4k_1^2}+\cfrac{20(4k_1^2+\cfrac{1}{4})}{4k_1^2+1}=\cfrac{100k_1^2+25}{1+4k_1^2}=25$
练习:
1、设点$A(x_1,y_1)B(x_2,y_2)$是椭圆$\cfrac{x^2}{4}+y^2=1$上两点,若过点A,B且斜率分别为$-\cfrac{x_1}{4y_1},-\cfrac{x_2}{4y_2}$的两条直线交于点P,且直线OA,OB的斜率之积为$-\cfrac{1}{4},E(\sqrt{6},0),\left | PE\right |的最小值为(\qquad)$
难度较大,要求出$P的轨迹方程\cfrac{x^2}{8}+\cfrac{y^2}{2}=1$,要求用参数方程设出$A(2\cos \alpha ,\sin \alpha ),B(\cos\beta ,sin \beta )$,还要对椭圆方程求导,求出切线方程,才能得到A,B点为椭圆的切线PA,PB的切点。写出PA,PB的直线方程。
解:$A(2\cos \alpha ,\sin \alpha ),B(\cos\beta ,sin \beta ),对\cfrac{x^2}{4}+y^2=1两边求导,有\cfrac{2x}{4}+2y {y}' =0\Rightarrow {y}' =-\cfrac{x}{4y}$,可见PA,PB为椭圆的切线,A,B为切点。
则直线AP的方程为$\cfrac{x_1x}{4}+ y_1y=1 \Rightarrow \cfrac{ x\cos \alpha}{2}+ y\sin \alpha=1\quad ①$
同理BP的方程为$\cfrac{x_2x}{4}+ y_2y=1 \Rightarrow \cfrac{ x\cos \beta}{2}+ y\sin \beta=1\quad ②$
$①\cdot \sin \beta - ②\cdot \sin \alpha\Rightarrow x_P=\cfrac{2(\sin \beta -\sin \alpha)}{\sin (\beta -\alpha)}$
$①\cdot \cos \beta - ②\cdot \cos \alpha\Rightarrow y_P=\cfrac{\cos \beta -\cos \alpha}{\sin (\alpha-\beta)}$
$\cfrac{x_P^2}{4}+y_p^2=\cfrac{(\sin \beta -\sin \alpha)^2-(\cos \beta -\cos \alpha)^2}{\sin^2(\beta-\alpha)}=\cfrac{2-2\cos (\alpha-\beta) }{\sin^2(\beta-\alpha)}$
$又\because k_{OA}k_{OB}=\cfrac{\sin \alpha}{2\cos\alpha }\cdot \cfrac{\sin \beta}{2\cos\beta }=-\cfrac{1}{4}\Rightarrow \cos(\alpha-\beta )=0\Rightarrow \sin (\alpha-\beta )=\pm 1\Rightarrow \cfrac{x_P^2}{4}+y_p^2=2$
所以P点的轨迹方程为:$\cfrac{x^2}{8}+\cfrac{y^2}{2}=1,设P(2\sqrt{2}\cos \theta ,\sqrt{2}\sin \theta )到E(\sqrt{6},0)$的距离,
$|PE|=\sqrt{(2\sqrt{2}\cos \theta -\sqrt{6})^2+(\sqrt{2}\sin \theta )^2}=\sqrt{6\cos^2\theta -8\sqrt{3}\cos\theta +8}=|\sqrt{6}\cos\theta -2\sqrt{2}|$
$当\cos\theta=1,|PE|_{min}=2\sqrt{2}-\sqrt{6}$
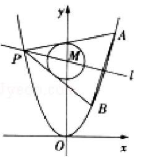
2、浙江2011年21题。已知抛物线$C_1:x^2=y,圆C_2:x^2+(y-4)^2=1$圆心为点M。
(1)求点$M$到抛物线$C_1$准线的距离。
(2)已知点$P是C_1$上一点(异于原点),过点$P$作圆$C_2$的两条切线,交抛物线$C_1$于$A,B$两点,若过$M,P$的直线$l$垂直于A,B,求$l$的方程。
3、
4、
5、
6、




