$1、在复平面内，复数z=(2+i)i对应的点位于第几象限；$
$2、已知集合A=\{x|-1\le x\le 2,x\in Z\},B=\{x|\cfrac{1}{x}\le 1\},A\cap B=$
$5、 已知\cfrac{\cos 2\theta}{\cos (\theta-\cfrac{\pi}{4})}=\cfrac{\sqrt{2}}{2},则\sin 2\theta$
$解：\cfrac{\cos^2\theta -\sin^2\theta}{\cos\theta +\sin\theta}=(\cfrac{\sqrt{2}}{2})^2\Rightarrow \cos \theta-\sin \theta=0.5\Rightarrow 1-\sin 2\theta=\cfrac{1}{4}$

$15、在\triangle ABC中,角A,B,C的对边分别为a,b,c,ab\cos C+ac\cos B=bc\sin A.$
$(1)证明:\sin A=\sin B\sin C$
$(2)若\tan B=2\tan C，求\tan A$
$证明:(1)\cfrac{2S_\triangle}{\sin C}\cos C+\cfrac{2S_\triangle}{\sin B}\cos B=2S_\triangle\Rightarrow \cfrac{\cos C}{\sin C}+\cfrac{\cos B}{\sin B}=1$
$\Rightarrow \cfrac{\sin B\cos C+\cos B\sin C}{\sin B\sin C}=1\Rightarrow \sin A=\sin (B+C)=\sin B\sin C$
$(2)-\tan A=\tan(\pi- A)=\tan(B+C)=\cfrac{\tan B +\tan C}{1-\tan B\tan C}$
$\Rightarrow \tan A+\tan B+\tan C=\tan A\tan B\tan C\quad 正切恒等式$
$\because \sin A=\sin (B+C)=\sin B\cos C+\cos B\sin C=\sin B\sin C$
$\times \cos B\cos C,得\tan B+\tan C=\tan B\tan C\Rightarrow 3\tan C=2\tan^2 C\Rightarrow \tan C=\cfrac{3}{2}$
$\tan A+3\tan C=\tan A\times 2\tan^2C\Rightarrow \tan A=\cfrac{7}{2}$

$解法二:\cfrac{a}{\sin A}=\cfrac{b}{\sin B}=\cfrac{c}{\sin C}\Rightarrow b\sin A=a\sin B
\quad bc\sin A=ac\sin B=ab\sin C左边$
$ac\sin B=ab\cos C+ac\cos B \Rightarrow c\sin B=b\cos C+c\cos B\Rightarrow\sin B\cos C+\cos B\sin C=\sin B\sin C$
$\Rightarrow \sin(B+C)=\sin B\sin C\Rightarrow \sin A=\sin(B+C)=\sin B\sin C$
$a\sin B\cos C+a\cos B\sin C=a\sin B\sin C \Rightarrow \sin B\cos C+\cos B\sin C=\sin B\sin C$
$两边{\div} \cos B\cos C,得\tan B+\tan C=\tan B\tan C\quad \tan B=2 \tan C\Rightarrow 3\tan C=2\tan^2C$
$\Rightarrow \tan C=\cfrac{3}{2},\tan B=3,-\tan A=\tan (\pi-A)=\tan (B+C)=\cfrac{\tan B+\tan C}{1-\tan B\tan C}= $

$16、已知椭圆C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)的左顶点A为(-2,0)，且离心率为\cfrac{\sqrt{3}}{2}.$
$(1)求椭圆方程:\cfrac{x^2}{4}+y^2=1$
$(2)过点(6,0)的直线l交于不同的两点PQ(异于A），记直线AP,AQ的斜率分别为k_1,k_2,求k_1k_2$
$解：点乘双根法能大大减少此题的计算量。$
$设P(x_1,y_1)Q(x_2,y_2),求k_1k_2=\cfrac{y_1y_2}{(x_1+2)(x_2+2)},x_1,x_2,y_1,y_2是直线l$方程与椭圆方程的公共解。
$\begin{cases}直线l:y=k(x-6)\quad 正设直线\\ \qquad \\椭圆C:x^2+4y^2-4=0\end{cases}\Rightarrow x^2+4k^2(x-6)^2-4=0\quad ①$
$因为x_1,x_2是①式的根，因此，上式可改写成:x^2+4k^2(x-6)^2-4＝(1+4k^2)(x_1-x)(x_2-x)$
$令x=-2,可得(x_1+2)(x_2+2)=\cfrac{64\times 4k^2}{1+4k^2}$
$\begin{cases} 直线l:\qquad x=my+6\quad 反设直线\\ 椭圆C:\quad x^2+4y^2-4=0\end{cases}\Rightarrow (my+6 )^2+4y^2-4=0\quad ②$
$因为y_1,y_2是②式的根，因此，上式可改写成:(my+6 )^2+4y^2-4＝(m^2+4)(y_1-y)(y_2-y)$
$令y=0,可得y_1y_2=\cfrac{32}{m^2+4}$
$\because k_1k_2=\cfrac{y_1y_2}{(x_1+2)(x_2+2)}=\cfrac{\cfrac{32}{m^2+4}}{\cfrac{64\times 4k^2}{1+4k^2}}\quad \because m=\cfrac{1}{k}\Rightarrow k_1k_2=\cfrac{1}{8}$

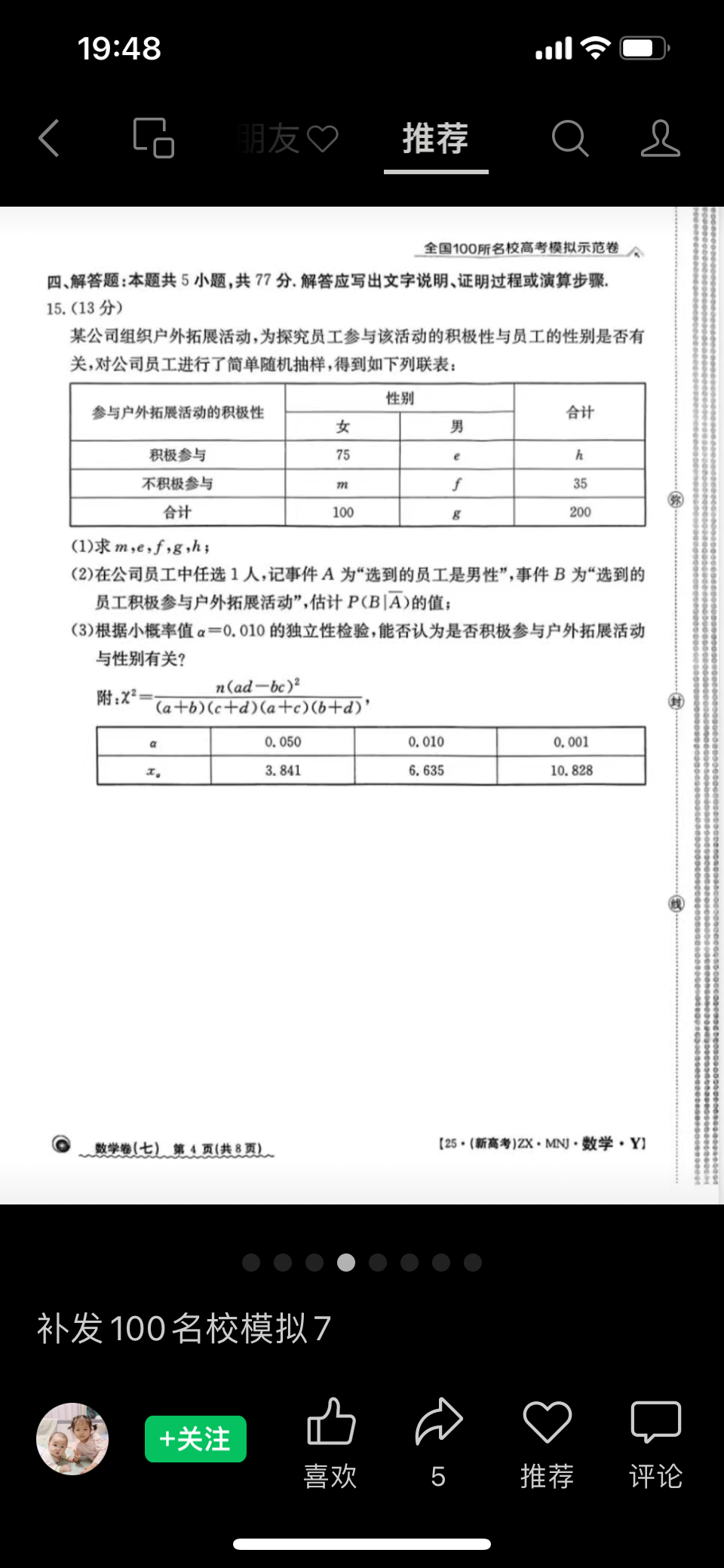
$17、已知函数f(x)=ax^2-x\ln x,a\in R$
$(1)若函数f(x)在定义域内单调递增，求的取值范围$
$(2)若过点(0,1)可作曲线y=f(x)的两条切线l_1，l_2，记直线l_1，l_2的斜率分别为k_1,k_2,求k_1+k_2的取值范围$
$解:{f}' (x)=2ax-1-\ln x\ge0\Rightarrow 2a\ge \cfrac{1+\ln x}{x}\quad $
$令g(x)= \cfrac{1+\ln x}{x}\Rightarrow {g}' (x)=\cfrac{-\ln x}{x^2}\quad$
$x\in (0,1) \quad {g}' (x)\gt 0,g(x)\nearrow ;\qquad x\in (1,+\infty ) \quad {g}' (x)\lt 0,g(x)\searrow ;$
$\therefore g(x)在x=1处有最大值g(1)=1,2a\ge 1\Rightarrow a\ge \cfrac{1}{2}$
$解:(2)设切点坐标为(t,t(at-\ln t)),切线斜率为{f}' (t)=2at-1-\ln t,故切线方程为:$
$y-t(at-\ln t)=(2at-1-\ln t)(x-t),切线经过(0,1)，故有1-t(at-\ln t)=-t(2at-1-\ln t)\Rightarrow$
$1-at^2+t\ln t=-2at^2+t+t\ln t,\Rightarrow at^2-t+1=0$
$由于x\gt 0，即切点坐标t\gt 0\therefore t_1+t_2=t_1t_2=\cfrac{1}{a},且a\gt 0\Rightarrow \Delta =1-4a\gt 0$
$0\lt a\lt \cfrac{1}{4},k_1+k_2=2a(t_1+t_2)-2-\ln(t_1+t+2)=2a\cfrac{1}{a}-2-\ln \cfrac{1}{a}=\ln a$
$0\lt a\lt \cfrac{1}{4},\therefore k_1+k_2=\ln a \in (-\infty,-2\ln2)$

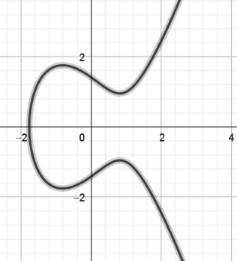
$18、如图所示，在长方体ABCD-A_1B_1C_1D_1中，点M,N分别是直线AB_1,BC_1上的动点。$
$(1)若M,N分别为线段AB_1,BC_1的中点，证明：MN//平面ABCD;$
$(2)若AB=BC=3,且二面角A-B_1D_1－C的斜弦值为\cfrac{1}{3}.$
$①求AA_1;$
$②若直线MN与平面ABCD所成角为\cfrac{\pi}{3}，求线段MN长度的最小值。$
$解:(1)证明：以D为坐标原点，DA,DC,DD_1分别为x,y,z$轴正方向，建立空间直角坐标系,令$DA=a,DC=b,DD_1=C,$
$则A(a,0,0),B_1(a,b,c),B(a,b,0),C(0,b,c),M(a,\cfrac{b}{2},\cfrac{c}{2}),N(\cfrac{a}{2},b,\cfrac{c}{2}),\overrightarrow{MN}=(-\cfrac{a}{2},\cfrac{b}{2},0)$
$显然平面ABCD的法向量为\vec{n} =(0,0,1),\vec{n}\cdot \overrightarrow{MN}=0,所以MN//平面ABCD $
$(2)解①A(3,0,0),B_1(3,3,c),C(0,3,0),D_1(0,0,C),\overrightarrow{AB_1}=(0,3,0),\overrightarrow{D_1B_1}=(3,3,0),\overrightarrow{CB_1}=(3,0,0)$
$平面AB_1D_1的法向量为\vec{n_1}:得\vec{n_1}\cdot \overrightarrow{AB_1}=0,\vec{n_1}\cdot \overrightarrow{D_1B_1}=0，解得\vec{n_1}=(c,-c,3)$
$平面CB_1D_1的法向量为\vec{n_2}:得\vec{n_2}\cdot \overrightarrow{CB_1}=0,\vec{n_2}\cdot \overrightarrow{D_1B_1}=0，解得\vec{n_2}=(-c,c,3)$
$\cos <\vec{n_1},\vec{n_2}>=\cfrac{\vec{n_1}\cdot\vec{n_2}}{|\vec{n_1}|\times|\vec{n_2}|}=\cfrac{|9-2c^2|}{2c^2+9}=\cfrac{1}{3},3(2c^2-9)=2c^2+9\Rightarrow c=3$
$3(9-2c^2)=2c^2+9\Rightarrow c=\cfrac{3}{2},此夹角为钝角，舍去,故可得AA_1=3$
$解②,A(3,0,0),B(3,3,0),B_1(3,3,3),C_1(0,3,3),\quad\therefore \overrightarrow{AB}=(0,3,0),\overrightarrow{AB_1}=(0,3,3),\overrightarrow{BC_1}=(-3,0,3)$
$设\overrightarrow{AM}=\lambda\overrightarrow{AB_1},\overrightarrow{BN}=\mu\overrightarrow{BC_1},\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{BN}-\overrightarrow{AM}=(0,3,0)+\mu (-3,0,3)-\lambda (0,3,3)$
$\overrightarrow{MN}=(-3\mu,3=3\lambda,-3\lambda +3\mu)=-3(\mu,\lambda -1,\mu -\lambda),平面ABCD的法向量\vec{n}=(0,0,1)$
$\sin\cfrac{\pi}{3}=\cfrac{\sqrt{3}}{2}=\cfrac{\vec{n}\cdot \overrightarrow{MN}}{|\vec{n}||\overrightarrow{MN}|}=\cfrac{3|\mu -\lambda|}{3\sqrt{\mu^2+(\lambda-1)^2+(\mu-\lambda)^2}}$
$分析：求MN的最小值，即求3\sqrt{\mu^2+(\lambda-1)^2+(\mu-\lambda)^2}=\cfrac{3|\mu -\lambda|}{\cfrac{\sqrt{3}}{2}}=2\sqrt{3}|\mu -\lambda|的最小值，$
$由上式可知即求|\mu-\lambda|的最小值。上等式包含\mu与\lambda之间的关系，要求最值，可用\Delta法,即令t=\mu-\lambda$
$\cfrac{3}{4}=\cfrac{(\mu-\lambda)^2}{\mu^2+(\lambda-1)^2+(\mu -\lambda)^2}\Rightarrow 4\mu ^2-8\mu\lambda +4\lambda ^2 =3\mu ^2+3\lambda ^2-6\lambda +3+3\mu ^2-6\mu \lambda +3\lambda ^2$
$\Rightarrow 2\mu^2+2\lambda ^2 +2\mu \lambda -6\lambda +3=0,{\color{Red} t=\mu-\lambda,\mu=t+\lambda代入上式} $
$2(t+\lambda)^2+2\lambda ^2 +2(t+\lambda) \lambda -6\lambda +3, 展开整理为关于\lambda的一元二次方程：$
$6\lambda^2+6(t-1)\lambda+t^2+3=0,因为\lambda\in R,\Delta\ge 0,可得36(t-1)^2-4\times 6\times (t^2+3)\ge 0$
$t^2+6t+3\le 0,-3-\sqrt{6}\le t\le -3+\sqrt{6},{\color{Red} \quad\therefore 2\sqrt{3}|t|_{min}=} 2\sqrt{3}(3-\sqrt{6})=6\sqrt{3}-6\sqrt{2}$
${\color{Red}解②法二： } 设M(3,m,m),N(n,3,3-n);A(3,0,0),B(3,3,0),\overrightarrow{AM}=(0,m,m),$
$\overrightarrow{BN}=(n-3,0,3-n),平面ABCD的法向量\vec{n}=(0,0,1)$
$\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{BN}-\overrightarrow{AM}=(0,3,0)+(n-3,0,3-n)-(0,m,m)=(n-3,3-m,3-n-m),$
$\sin \cfrac{\pi}{3}=\cfrac{\sqrt{3}}{2}=\cfrac{\vec{n}\cdot\overrightarrow{MN}}{|\vec{n}|\times|\overrightarrow{MN}|}=\cfrac{|3-n-m|}{\sqrt{(n-3)^2+(3-m)^2+(3-n-m)^2}}$
$\cfrac{3}{4}=\cfrac{(3-n-m)^2}{(n-3)^2+(3-m)^2+(3-n-m)^2}\Rightarrow 3[(n-3)^2+(3-m)^2+(3-n-m)^2]=4(3-n-m)^2$
$3(n-3)^2+3(m-3)^2=(3-n-m)^2,(n-3)^2+(m-3)^2\ge \cfrac{(6-n-m)^2}{2}$
$\Rightarrow (3-n-m)^2\ge \cfrac{3}{2}\times(3-n-m)^2,换元，令t=n+m$
$2(3-t)^2\ge 3(6-t)^2\Rightarrow t^2-24t+90\le 0\Rightarrow 12-3\sqrt{6}\le t\le 12+3\sqrt{6}$
$|\overrightarrow{MN}|=\cfrac{2\sqrt{3}}{3}|3-t|\Rightarrow 9-3\sqrt{6}\le t-3\le 9+3\sqrt{6}$
$\Rightarrow \cfrac{2\sqrt{3}}{3}(9-3\sqrt{6})\le \cfrac{2\sqrt{3}}{3}(t-3)\le \cfrac{2\sqrt{3}}{3}(9+3\sqrt{6})\Rightarrow 6(\sqrt{3}-\sqrt{2})\le |\overrightarrow{MN}|\le 6(\sqrt{3}+\sqrt{2})$
$故|\overrightarrow{MN}|最小值为6(\sqrt{3}-\sqrt{2})$

$1、泉州2026年若实数x,y,z满足2^x-2=3^y-3=5^z-5,则x,y,z的大小关系不可能是(\quad )$
$A.x=y=z\quad B.x\gt y\gt z\quad C.z\gt y\gt x\quad D.z\gt x\gt y$
$解：令2^x-2=3^y-3=5^z-5=k\Rightarrow \begin{cases} x=\log_{2}{(k+2)} \\y=\log_{3}{(k+3)} \\z=\log_{5}{(k+5)} \end{cases}若k=0,A成立；$
$若k=1,x=\log_{2}{3},y=\log_{3}{4},z=\log_{5}{6},则x\gt y\gt z,B成立$
$若k=－1,x=\log_{2}{1}＝0,y=\log_{3}{2},z=\log_{5}{4},\log_{2}{3}\gt\log_{4}{5},\Rightarrow \cfrac{1}{\log_{3}{2}}\gt\cfrac{1}{\log_{5}{4}}\Rightarrow 0\lt \log_{3}{2}\lt\log_{5}{4},故C正确$

$2、长郡2026年若实数x,y,z满足2^x-2=7^z-7=5^y-5,则x,y,z的大小关系不可能是(\quad B\quad )$
$A.x=y=z\quad B.z\gt x\gt y\quad C.z\gt y\gt x\quad D. x\gt y\gt z$

2025年高考8题若实数$x,y,z满足\log_{2}{x}+2=\log_{3}{y}+3=\log_{5}{z}+5,则x,y,z的大小关系不可能是(\quad )$
$A.x\gt y\gt z\quad B.x\gt z\gt y\quad C.y\gt x\gt z\quad D.y\gt z\gt x$
$解：令\log_{2}{x}+2=\log_{3}{y}+3=\log_{5}{z}+5=k\Rightarrow x=2^{k-2},y=x=3^{k-3},z=x=5^{k-5}$
$k=0,x=2^{-2}=\cfrac{1}{4},y=3^{-3}=\cfrac{1}{27},z=5^{-5}=\cfrac{1}{5^5},x\gt y\gt z,A$
$k=1,x=2^{-1}=\cfrac{1}{2},y=3^{-2}=\cfrac{1}{9},z=5^{-4}=\cfrac{1}{5^4},x\gt y\gt z,C$
$k=2,x=2^{0}=1,y=3^{-1}=\cfrac{1}{3},z=5^{-3}=\cfrac{1}{5^3},x\gt y\gt z,C$
$k=3,x=2^{1}=2,y=3^{0}=1,z=5^{-2}=\cfrac{1}{25},y\gt c\gt z,C$
$k=4,x=2^{2}=4,y=3^{1}=3,z=5^{-1}=\cfrac{1}{5},y\gt x\gt z,C$
$k=5,x=2^{3}=8,y=3^{2}=9,z=5^{0}=1,y\gt x\gt z,C$
$k=6,x=2^{4}=16,y=3^{3}=27,z=5^{1}=5,y\gt x\gt z,C$
$k=7,x=2^{5}=32,y=3^{4}=81,z=5^{2}=25,y\gt x\gt z,C$
$k=8,x=2^{6}=64,y=3^{5}=243,z=5^{3}=125,y\gt z\gt x,D$

$6.已知\cfrac{1}{\sin 10^o} -\cfrac{\lambda }{\cos 10^o} =4, 则\lambda (\qquad )$
$A.1\quad B.\sqrt{2},\quad C.2\quad D.\sqrt{3}$
$7.已知函数f(x)=e^x\ln a-ax(a\gt 1),若f(x)\ge 0恒成立 则实数a的值为(\qquad )$
$A.e\quad B.\sqrt{e},\quad C.e^2\quad D.e^{3}$
$8.在三棱锥A-BCD中,AD\perp 平面BCD,\angle ABD+\angle CBD=\cfrac{\pi}{2},且BD=BC=4$,则三棱锥$A-BCD$外接球表面积最小值为$(\qquad )$
$A.(8\sqrt{5}+4)\pi\quad B.(8\sqrt{5}+8)\pi,\quad C.(8\sqrt{5}-4)\pi\quad D.(8\sqrt{5}-8)\pi$
此题的计算相当于大题，可作为大题练习。棱锥外接球，要将棱锥补全为棱柱，上下底面外接圆圆心连线(即高)的中点为球心。
$设\angle CBD=\alpha ,故\angle ABD=\cfrac{\pi}{2} -\alpha$
$CD^2=4^2+4^2-2\times 4\times 4\times\cos \alpha \Rightarrow CD^2=32(1-\cos \alpha )$
$\cfrac{CD}{\sin \alpha }=2r\Rightarrow r=\cfrac{CD}{2\sin \alpha } \Rightarrow r^2=\cfrac{CD^2}{4\sin^2 \alpha }=\cfrac{8(1-\cos \alpha )}{\sin^2\alpha }$
$\cfrac{AD}{4}=\tan (\cfrac{\pi}{2}-\alpha )=\cfrac{\sin(\cfrac{\pi}{2}-\alpha ) }{\cos(\cfrac{\pi}{2}-\alpha )}=\cfrac{1}{\tan \alpha} \Rightarrow \cfrac{AD}{2}=\cfrac{2}{\tan \alpha}$
$(\cfrac{AD}{2})^2=\cfrac{4}{\tan^2 \alpha},R^2=r^2+(\cfrac{AD}{2})^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{\sin^2 \alpha}=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}$
此时分子分母均为含$\cos \alpha$的两次项，先分离常数，变成分子为一次项，分母为二次项，再对分子整体换元。
$R^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}=-4+\cfrac{ -8\cos \alpha +12}{1-\cos^2 \alpha}=-4\cfrac{ 4(-2\cos \alpha +3)}{1-\cos^2 \alpha}$
$令 t=3-2\cos \alpha \in (1,3)\Rightarrow \cos^2 \alpha=\cfrac{1}{4}(3-t)^2,1- \cos^2 \alpha=-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}$
$R^2=f(t)=-4+\cfrac{4t}{-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}}=-4+\cfrac{-16t}{t^2-6t+5}=-4+\cfrac{-16}{t-6+\cfrac{5}{t}}$
$t+\cfrac{5}{t}-6\ge 2\sqrt{5}-6\Rightarrow \cfrac{1}{t+\cfrac{5}{t}-6}\le \cfrac{1}{2\sqrt{5}-6}
\Rightarrow \cfrac{-16}{t+\cfrac{5}{t}-6}\ge \cfrac{-16}{2\sqrt{5}-6}=\cfrac{8}{3-\sqrt{5}}=6+2\sqrt{5}$
$\Rightarrow R^2=-4+6+2\sqrt{5}=2+2\sqrt{5},S=4\pi R^2=(8+8\sqrt{5})\pi$

10.棱长为2的正方体$ABCD-A_1B_1C_1D_1$中，P,Q分别是棱$CC_1,BC$的中点，动点M满足$\vec{DM}=\lambda \vec{DA} +\mu \vec{DD_1},其中\lambda ,\mu \in R$,则下列结论正确的是$(\qquad ABD)$
$A.若\lambda +\mu=1，则CM\perp DB_1;$
$B.若\lambda =\mu,则三棱锥B_1-AMC体积为定值;$
$C.若0\le\lambda\le 1 ,\mu=0.5,则直线PM与BC所成的角最小值为\cfrac{\pi}{3} ;$
$D.若动点M在三棱锥C-DPQ外接球上的表面上，则动点轨迹长度为\sqrt{2}\pi $
$解: A易证证。B选，M$为动点，不要以$M$所在的平面为底，要以$M$为棱锥的顶点。即三棱锥${\color{Red}M-ACB_1},M在对角线A_1D上，A_1D\parallel CB_1$
$C选，以D为坐标原点，DA,DC,DD_1为x,y,z轴建立坐标系，\overrightarrow{CB} =(2,0,0),\overrightarrow{PM}=(2\lambda ,-2,0)$
$\cos \alpha =\cfrac{\overrightarrow{CB}\cdot \overrightarrow{PM}}{|\overrightarrow{CB}|\times| \overrightarrow{PM}|}=\cfrac{\lambda }{\sqrt{\lambda ^2+1}}=\cfrac{1}{\sqrt{\cfrac{1}{\lambda ^2}+1}}\quad \lambda\in [0,1] \lambda=1时，\alpha=\cfrac{\pi}{4}$
$D.与上题一样，补全三棱锥{\color{Red} D-CPQ} $成三棱柱 ，动点M的轨迹为圆，即求圆的半径$r,PQ$为该圆的直径$,r=\cfrac{\sqrt{2}}{2},C=2\pi r= \sqrt{2}\pi$

11.如图，在一次社会实践中某学校数学探究实验组设计一个门把手，其 纵截面轮廓近似曲线$C：y^2=x^3-2x+2$的一部分，则$(\quad )$

A.点(1,1)在C上；
B.在(1,1)处的切线，其与C的交点的横坐标均为整数；
C.若C在x 轴上方的部分为函数f(x)的图象，则$x=\cfrac{\sqrt{6}}{3}是f(x)$的最小值点；
D.C在y轴左边的部分到坐标 原点O的距离均大于$\sqrt{2}$.

13. 如图，$4\times 6$的方格纸(小正方形的边长为1)中有一个向量$\vec{OA}$(以图中的格点O为起点，格点A为终点),则满足
    $\vec{OA}\cdot \vec{OB}=1$的格点B共有多少个。
    
    14.设数列$\{a_n\}$的前n项和为$S_n,a_1=1,且2S_n=a_{n+1}-1(n\in N^*)$.若对于任意的正整数n,都有$a_1b_n+a_2b_{n-1}+a_3b_{n-2}+...+a_nb_1=3^n-n$成立。则满足等式$b_1+b_2+b_3+...+b_n=a_n$的所有正数数$n$的和为
    17.已知正项数列$\{a_n\}满足n\lg a_{n+1}=(n+1)\lg a_n且a_1=3$;
    $(1)求数列\{a_n\}的通项公式；$
    $(2)设b_n=\cfrac{a_n-1}{a_n+1},数列\{b_n\}的前n项和为S_n，求[S_{2025}]$
    $解:n\lg a_{n+1}=(n+1)\lg a_n\Rightarrow \cfrac{\lg a_{n+1}}{n+1}=\cfrac{\lg a_{n}}{n}=\cfrac{\lg a_1}{1}=a_1$
    $\Rightarrow \lg a_n=n\lg 3\Rightarrow {\color{Red} a_n=3^n} $
    $b_n=\cfrac{a_n-1}{a_n+1}=\cfrac{3^n-1}{3^n+1}=\cfrac{3^n+1-2}{3^n+1}=1-\cfrac{2}{3^n+1}$
    $分析，S_{2025}=2025-(\cfrac{2}{3+1}+\cfrac{2}{3^2+1}+\cfrac{2}{3^3+1}+\cdots +\cfrac{2}{3^{2025}+1}),$
    $求\le S_{2025}的最大整数，即求后面的前2025项的和跟1和2比较大小。$
    $若和小于1，则结果为2024，若和小于2，大于1,则为2023$
    $(\cfrac{2}{3+1}+\cfrac{2}{3^2+1}+\cfrac{2}{3^3+1}+\cdots +\cfrac{2}{3^{2025}+1})=2(\cfrac{1}{3+1}+\cfrac{1}{3^2+1}+\cdots +\cfrac{1}{3^{2025}+1})$
    $\lt 2(\cfrac{1}{3}+\cfrac{1}{3^2}+\cdots +\cfrac{1}{3^{2025}})=2\cfrac{\cfrac{1}{3}-(\cfrac{1}{3})^{2025}}{1-\cfrac{1}{3}}\lt 2\cdot \cfrac{\cfrac{1}{3}}{\cfrac{2}{3}}=1$
    $[S_{2025}]=2025-1=2024$

抛物线$y=x^2$上异于坐标原点$O$的两个不同的动点$A,B满足OA\perp OB.\triangle AOB$的面积是否存在最小值。若存在，请求出最小值；若不存在，请说明理由。
解：设$A(x_1,y_1)B(x_2,y_2)$直线AB的方程为$y=kx+m$,联立$\begin{cases} y=kx+m\\y=x^2\end{cases} \Rightarrow　x^2-kx-m=0$
$x_1+x_2=k,x_1x_2=-m\quad \overrightarrow{OA} \cdot \overrightarrow{OB}=x_1x_2+y_1y_2=0$
$y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=-k^2m+k^2m+m^2=m^2$
$\overrightarrow{OA} \cdot \overrightarrow{OB}=x_1x_2+y_1y_2=-m+m^2=0\Rightarrow m=1或m=0舍去$
$故直线l_{AB}过定点(0,1)，y=kx+1$
以直线的定点为界，将$\triangle AOB$分成左右两部分，故$S_{\triangle AOB}=\cfrac{1}{2}\times 1\times |x_1-x_2|=\cfrac{1}{2}\sqrt{k^2+4}\ge 1$

引申1.若直线$l与椭圆C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)交于M,N$两点，A为椭圆的右顶点，且$AM\perp BN$.则直线$l过定点(\cfrac{e^2}{2-e^2}a,0)$
引申2.若直线$l与双曲线C:\cfrac{x^2}{a^2}－\cfrac{y^2}{b^2}=1(a\gt 0，b\gt 0)交于M,N$两点，A为双曲线的右顶点，且$AM\perp BN$.则直线$l过定点(\cfrac{e^2}{2-e^2}a,0)$
引申3.若直线$l与抛物线y^2=2px(p\gt 0)交于M,N$两点，A为抛物线顶点，且$AM\perp AN$.则直线$l过定点(2p,0)$