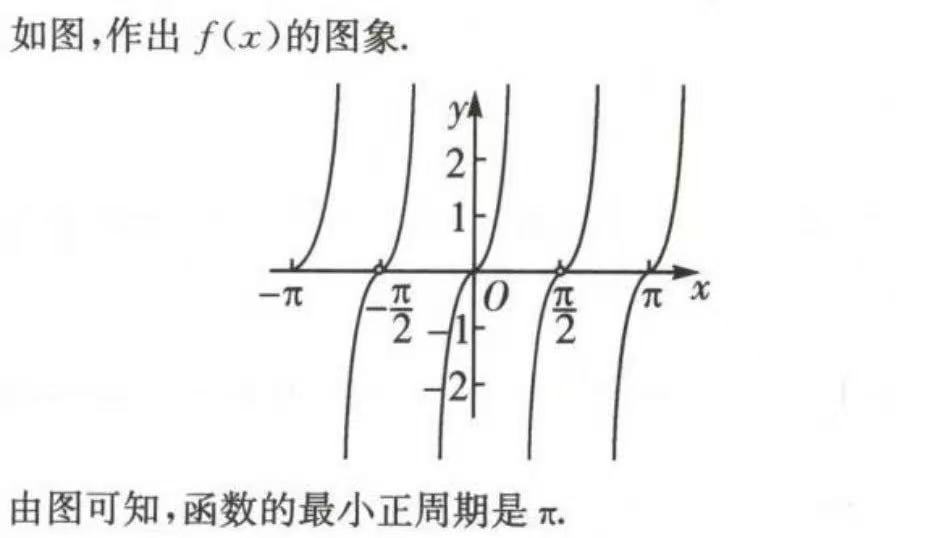
正切函数的周期

$1、函数f(x)=\cfrac{2\tan x}{1-\tan^2 x}的最小正周期是(\qquad)$
$A.\cfrac{\pi}{4}\quad B.\cfrac{\pi}{2}\quad C.\pi \quad D.2\pi$
$解:考查f(x)与\tan 2x的定义域，类似y=\cfrac{x^2}{x}=x$
$ 应用倍角公式化简得到 f(x)=\cfrac{2\tan x}{1-\tan^2 x}=\tan 2x ，\tan 2x的周期为\cfrac{\pi}{2},且在x=k\pi \pm\cfrac{\pi}{2}有定义，$
$但f(x)在x=k\pi \pm\cfrac{\pi}{2}处无定义,亦即f(x)化简后扩大了定义域，根据周期函数的对称性，$
故周期为$\pi$

$2、2026年T8联考第15题，在\triangle ABC中，角A,B,C所对边分别为a,b,c,且满足\cos^2\cfrac{A}{2}=\cfrac{b+c}{2c}.$
$①求角C的大小。直角，第二问初中要求$
$②若点D在AB边上，且满足AB=3AD,求\cfrac{\tan A}{\tan \angle ACD}$

--

${\color{Red} 3、} 已知函数f(x)\begin{cases} e^x(2x-1),\quad x\gt 0,\\k(x+1),\quad x\lt 0\end{cases},g(x)=f(x)+f(-x),$
$若函数g(x)恰好有4个零点，则实数k的取值范围是(\qquad)$
$A.(-\infty,1）\quad B.(1,4e^{\cfrac{3}{2}})\quad C.(4e^{\cfrac{3}{2}},+\infty)\quad D.(1,+\infty)$
$令g(x)=0,即f(x)=-f(-x),-f(-x)即是f(x)的中心对称图形。即x\gt 0时e^x(2x-1)与 k(x-1)有两点交点,相切时临界$
$x\gt 0時，{\color{Red}{f}' (x)=e^x(2x+1) } ,设(x_0,y_0)是两曲线的切点，\begin{cases} y_0=k(x_0-1)\qquad \qquad\quad ①\\y_0=e^{x_0}(2x_0-1)\quad\qquad\quad ②\\k={f}'(x_0)=e^{x_0}(2x_0+1)\quad ③\end{cases}$
$ ③代入①,①②左边相等，2x_0-1=(2x_0+1)(x_0-1)\Rightarrow x_0=\cfrac{3}{2},x_0=0(舍去),回代③式k\gt 4e^{\cfrac{3}{2}}$

$4、已知a\gt 0,b\gt 0,\sqrt{ab}=\cfrac{1}{a}+\cfrac{1}{b}，则\cfrac{1}{\log_a 2}+\cfrac{1}{\log_b 2}最小值是(\qquad)$
$A.3\quad B.2\quad C.\sqrt{2}\quad D.1$

$5、已知函数f(x)=(x+a)(2^x-b),若f(x)\ge 0恒成立，则b+2^a的最小值是(\qquad)$
$A.-2\quad B.0\quad C.\sqrt{2}\quad D.2$

$6、等差数列\{a_n\}的前n项和为S_n,已知a_5=8,S_5=20,设b_n=\cfrac{\sin 2}{\cos a_n\cos a_{n+1}},则数列\{b_n\}的前n项和为$_
$解:\because a_n=a_1+(n-1)d=a_n-(n-1)d;S_n=na_1+\cfrac{1}{2}n(n-1)d=na_n-\cfrac{1}{2}n(n-1)d$
$\therefore S_5=na_5-\cfrac{1}{2}\times 5\times 4\times d\Rightarrow 20=40-10d,d=2$
$b_n=\cfrac{\sin 2}{\cos a_n\cos a_{n+1}}=\cfrac{\sin (a_{n+1}-a_n)}{\cos a_n\cos a_{n+1}}=\cfrac{\sin a_{n+1}\cos a_n-\cos a_{n+1}\sin a_n}{\cos a_n\cos a_{n+1}}=\tan a_{n+1}-\tan a_n$
$T_n=b_1+b_2+b_3+\cdots +b_n=\tan a_{n+1}-\tan a_1$

$作业:已知数列\{a_n\}中，a_2=1,设S_n为\{a_n\}的前n项和，2S_n=na_n$
$(1)求\{a_n\}的通项公式；$
$(2)设b_n=\cfrac{\sin 1}{\cos (a_n+1)\cos (a_{n+1}+1)},则数列\{b_n\}的前n项和T_n$

$7、已知数列\{a_n\}的前n项和为S_n.且满足a_1=-5,a_n=\cfrac{S_n}{n}+2(n-1),$
$若对于任意n\in N^*,\lambda\le S_n怛成立，则实数\lambda的取值范围是(\quad )$
$A.(-\infty,-6]\quad B.(-\infty,-5]\quad C.(-\infty,-3]\quad D.(-\infty,-2]$

${\color{Red} 8、}共零点变形题，x(\ln x+2)\le ax^2+\cfrac{2}{a}\ln x对\forall x\ge e恒成立，则实数a的取值范围是(\qquad)$
$a\lt 0(舍去)因为右边等式为负数。a\gt 0时，x\ln x+2x-ax^2-\cfrac{2}{a}\ln x\le 0\Rightarrow (x-\cfrac{2}{a})\ln x+x(2-ax)\le 0$
$\Rightarrow (ax-2)\ln x-ax(ax-2)\le 0\Rightarrow (ax-2)(\ln x-ax)\le 0$
$①容易得到a\ge \cfrac{1}{e}时，ln x\le ax,即ln x-ax\le 0,此时只要ax-2\ge 0即可，\because x\gt e,\Rightarrow a\ge\cfrac{2}{x}\Rightarrow a\ge \cfrac{2}{e}$
$②0\lt a\lt \cfrac{1}{e},\because \quad x\gt e, ⑴e\lt x \lt x_0,\ln x-ax\ge 0;⑵x\gt x_0,\ln x -ax\le 0,此时y=ax-2与y=\ln x-ax共零点x_0。$
$\ln x_0=ax_0=2,\Rightarrow x_0=e^2,x\in [e,e^2],ax-2\le 0,\ln x-ax\ge 0,(ax-2)(\ln x-ax)\le 0;$
$x\gt e^2,ax-x\ge 0,\ln x-ax\le 0,\Rightarrow (ax-2)(\ln x-ax)\le 0$
$综上述，a\in \{e^2\}\cup [\cfrac{1}{e},+\infty)$

${\color{Red} 9、}若关于x的不等式ax^2-ax\ln a-e^x\ln x\gt 0对\forall x\in (0,1)恒成立，则实数a的取值范围为(\qquad)$
$解:ax^2-ax\ln a-e^x\ln x\gt 0\Rightarrow x^2-x\ln a-\cfrac{e^x}{a}\ln x\gt 0\Rightarrow x(x-\ln a)\gt e^{x-\ln a}\ln x\Rightarrow$
$\cfrac{x-\ln a}{e^{x-\ln a}}\gt \cfrac{\ln x}{x}\quad 令f(x)=\cfrac{x}{e^x},上式等价于f(x-\ln a)\gt f(\ln x)\quad \forall x\in (0,1),\ln x\lt 0,,\Rightarrow x-\ln a\gt \ln x$
$x-\ln x\gt \ln a\Rightarrow \ln a\lt x-\ln x\quad (x\in (0,1)),易求导得x-\ln x在(0,1)单调递减$
$(x-\ln x)_{max}=1,a\le 1$