惠州六校联考
$6.已知\cfrac{1}{\sin 10^o} -\cfrac{\lambda }{\cos 10^o} =4, 则\lambda (\qquad )$
$A.1\quad B.\sqrt{2},\quad C.2\quad D.\sqrt{3}$
$7.已知函数f(x)=e^x\ln a-ax(a\gt 1),若f(x)\ge 0恒成立 则实数a的值为(\qquad )$
$A.e\quad B.\sqrt{e},\quad C.e^2\quad D.e^{3}$
$8.在三棱锥A-BCD中,AD\perp 平面BCD,\angle ABD+\angle CBD=\cfrac{\pi}{2},且BD=BC=4$,则三棱锥$A-BCD$外接球表面积最小值为$(\qquad )$
$A.(8\sqrt{5}+4)\pi\quad B.(8\sqrt{5}+8)\pi,\quad C.(8\sqrt{5}-4)\pi\quad D.(8\sqrt{5}-8)\pi$
此题的计算相当于大题，可作为大题练习。棱锥外接球，要将棱锥补全为棱柱，上下底面外接圆圆心连线(即高)的中点为球心。
$设\angle CBD=\alpha ,故\angle ABD=\cfrac{\pi}{2} -\alpha$
$CD^2=4^2+4^2-2\times 4\times 4\times\cos \alpha \Rightarrow CD^2=32(1-\cos \alpha )$
$\cfrac{CD}{\sin \alpha }=2r\Rightarrow r=\cfrac{CD}{2\sin \alpha } \Rightarrow r^2=\cfrac{CD^2}{4\sin^2 \alpha }=\cfrac{8(1-\cos \alpha )}{\sin^2\alpha }$
$\cfrac{AD}{4}=\tan (\cfrac{\pi}{2}-\alpha )=\cfrac{\sin(\cfrac{\pi}{2}-\alpha ) }{\cos(\cfrac{\pi}{2}-\alpha )}=\cfrac{1}{\tan \alpha} \Rightarrow \cfrac{AD}{2}=\cfrac{2}{\tan \alpha}$
$(\cfrac{AD}{2})^2=\cfrac{4}{\tan^2 \alpha},R^2=r^2+(\cfrac{AD}{2})^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{\sin^2 \alpha}=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}$
此时分子分母均为含$\cos \alpha$的两次项，先分离常数，变成分子为一次项，分母为二次项，再对分子整体换元。
$R^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}=-4+\cfrac{ -8\cos \alpha +12}{1-\cos^2 \alpha}=-4\cfrac{ 4(-2\cos \alpha +3)}{1-\cos^2 \alpha}$
$令 t=3-2\cos \alpha \in (1,3)\Rightarrow \cos^2 \alpha=\cfrac{1}{4}(3-t)^2,1- \cos^2 \alpha=-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}$
$R^2=f(t)=-4+\cfrac{4t}{-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}}=-4+\cfrac{-16t}{t^2-6t+5}=-4+\cfrac{-16}{t-6+\cfrac{5}{t}}$
$t+\cfrac{5}{t}-6\ge 2\sqrt{5}-6\Rightarrow \cfrac{1}{t+\cfrac{5}{t}-6}\le \cfrac{1}{2\sqrt{5}-6}
\Rightarrow \cfrac{-16}{t+\cfrac{5}{t}-6}\ge \cfrac{-16}{2\sqrt{5}-6}=\cfrac{8}{3-\sqrt{5}}=6+2\sqrt{5}$
$\Rightarrow R^2=-4+6+2\sqrt{5}=2+2\sqrt{5},S=4\pi R^2=(8+8\sqrt{5})\pi$
10.棱长为2的正方体$ABCD-A_1B_1C_1D_1$中，P,Q分别是棱$CC_1,BC$的中点，动点M满足$\vec{DM}=\lambda \vec{DA} +\mu \vec{DD_1},其中\lambda ,\mu \in R$,则下列结论正确的是$(\qquad ABD)$
$A.若\lambda +\mu=1，则CM\perp DB_1;$
$B.若\lambda =\mu,则三棱锥B_1-AMC体积为定值;$
$C.若0\le\lambda\le 1 ,\mu=0.5,则直线PM与BC所成的角最小值为\cfrac{\pi}{3} ;$
$D.若动点M在三棱锥C-DPQ外接球上的表面上，则动点轨迹长度为\sqrt{2}\pi $
$解: A易证证。B选，M$为动点，不要以$M$所在的平面为底，要以$M$为棱锥的顶点。即三棱锥${\color{Red}M-ACB_1},M在对角线A_1D上，A_1D\parallel CB_1$
$C选，以D为坐标原点，DA,DC,DD_1为x,y,z轴建立坐标系，\overrightarrow{CB} =(2,0,0),\overrightarrow{PM}=(2\lambda ,-2,0)$
$\cos \alpha =\cfrac{\overrightarrow{CB}\cdot \overrightarrow{PM}}{|\overrightarrow{CB}|\times| \overrightarrow{PM}|}=\cfrac{\lambda }{\sqrt{\lambda ^2+1}}=\cfrac{1}{\sqrt{\cfrac{1}{\lambda ^2}+1}}\quad \lambda\in [0,1] \lambda=1时，\alpha=\cfrac{\pi}{4}$
$D.与上题一样，补全三棱锥{\color{Red} D-CPQ} $成三棱柱 ，动点M的轨迹为圆，即求圆的半径$r,PQ$为该圆的直径$,r=\cfrac{\sqrt{2}}{2},C=2\pi r= \sqrt{2}\pi$
11.如图，在一次社会实践中某学校数学探究实验组设计一个门把手，其 纵截面轮廓近似曲线$C：y^2=x^3-2x+2$的一部分，则$(\quad )$
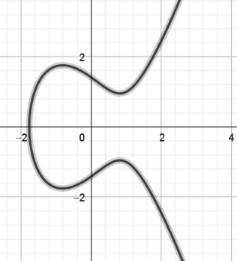
A.点(1,1)在C上；
B.在(1,1)处的切线，其与C的交点的横坐标均为整数；
C.若C在x 轴上方的部分为函数f(x)的图象，则$x=\cfrac{\sqrt{6}}{3}是f(x)$的最小值点；
D.C在y轴左边的部分到坐标 原点O的距离均大于$\sqrt{2}$.
- 如图，$4\times 6$的方格纸(小正方形的边长为1)中有一个向量$\vec{OA}$(以图中的格点O为起点，格点A为终点),则满足
$\vec{OA}\cdot \vec{OB}=1$的格点B共有多少个。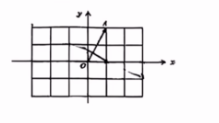
14.设数列$\{a_n\}$的前n项和为$S_n,a_1=1,且2S_n=a_{n+1}-1(n\in N^*)$.若对于任意的正整数n,都有$a_1b_n+a_2b_{n-1}+a_3b_{n-2}+...+a_nb_1=3^n-n$成立。则满足等式$b_1+b_2+b_3+...+b_n=a_n$的所有正数数$n$的和为
17.已知正项数列$\{a_n\}满足n\lg a_{n+1}=(n+1)\lg a_n且a_1=3$;
$(1)求数列\{a_n\}的通项公式；$
$(2)设b_n=\cfrac{a_n-1}{a_n+1},数列\{b_n\}的前n项和为S_n，求[S_{2025}]$