$1、泉州2026年若实数x,y,z满足2^x-2=3^y-3=5^z-5,则x,y,z的大小关系不可能是(\quad )$
$A.x=y=z\quad B.x\gt y\gt z\quad C.z\gt y\gt x\quad D.z\gt x\gt y$
$解：令2^x-2=3^y-3=5^z-5=k\Rightarrow \begin{cases} x=\log_{2}{(k+2)} \\y=\log_{3}{(k+3)} \\z=\log_{5}{(k+5)} \end{cases}若k=0,A成立；$
$若k=1,x=\log_{2}{3},y=\log_{3}{4},z=\log_{5}{6},则x\gt y\gt z,B成立$
$若k=－1,x=\log_{2}{1}＝0,y=\log_{3}{2},z=\log_{5}{4},\log_{2}{3}\gt\log_{4}{5},\Rightarrow \cfrac{1}{\log_{3}{2}}\gt\cfrac{1}{\log_{5}{4}}\Rightarrow 0\lt \log_{3}{2}\lt\log_{5}{4},故C正确$

$2、长郡2026年若实数x,y,z满足2^x-2=7^z-7=5^y-5,则x,y,z的大小关系不可能是(\quad B\quad )$
$A.x=y=z\quad B.z\gt x\gt y\quad C.z\gt y\gt x\quad D. x\gt y\gt z$

2025年高考8题若实数$x,y,z满足\log_{2}{x}+2=\log_{3}{y}+3=\log_{5}{z}+5,则x,y,z的大小关系不可能是(\quad )$
$A.x\gt y\gt z\quad B.x\gt z\gt y\quad C.y\gt x\gt z\quad D.y\gt z\gt x$
$解：令\log_{2}{x}+2=\log_{3}{y}+3=\log_{5}{z}+5=k\Rightarrow x=2^{k-2},y=x=3^{k-3},z=x=5^{k-5}$
$k=0,x=2^{-2}=\cfrac{1}{4},y=3^{-3}=\cfrac{1}{27},z=5^{-5}=\cfrac{1}{5^5},x\gt y\gt z,A$
$k=1,x=2^{-1}=\cfrac{1}{2},y=3^{-2}=\cfrac{1}{9},z=5^{-4}=\cfrac{1}{5^4},x\gt y\gt z,C$
$k=2,x=2^{0}=1,y=3^{-1}=\cfrac{1}{3},z=5^{-3}=\cfrac{1}{5^3},x\gt y\gt z,C$
$k=3,x=2^{1}=2,y=3^{0}=1,z=5^{-2}=\cfrac{1}{25},y\gt c\gt z,C$
$k=4,x=2^{2}=4,y=3^{1}=3,z=5^{-1}=\cfrac{1}{5},y\gt x\gt z,C$
$k=5,x=2^{3}=8,y=3^{2}=9,z=5^{0}=1,y\gt x\gt z,C$
$k=6,x=2^{4}=16,y=3^{3}=27,z=5^{1}=5,y\gt x\gt z,C$
$k=7,x=2^{5}=32,y=3^{4}=81,z=5^{2}=25,y\gt x\gt z,C$
$k=8,x=2^{6}=64,y=3^{5}=243,z=5^{3}=125,y\gt z\gt x,D$

$6.已知\cfrac{1}{\sin 10^o} -\cfrac{\lambda }{\cos 10^o} =4, 则\lambda (\qquad )$
$A.1\quad B.\sqrt{2},\quad C.2\quad D.\sqrt{3}$
$7.已知函数f(x)=e^x\ln a-ax(a\gt 1),若f(x)\ge 0恒成立 则实数a的值为(\qquad )$
$A.e\quad B.\sqrt{e},\quad C.e^2\quad D.e^{3}$
$8.在三棱锥A-BCD中,AD\perp 平面BCD,\angle ABD+\angle CBD=\cfrac{\pi}{2},且BD=BC=4$,则三棱锥$A-BCD$外接球表面积最小值为$(\qquad )$
$A.(8\sqrt{5}+4)\pi\quad B.(8\sqrt{5}+8)\pi,\quad C.(8\sqrt{5}-4)\pi\quad D.(8\sqrt{5}-8)\pi$
此题的计算相当于大题，可作为大题练习。棱锥外接球，要将棱锥补全为棱柱，上下底面外接圆圆心连线(即高)的中点为球心。
$设\angle CBD=\alpha ,故\angle ABD=\cfrac{\pi}{2} -\alpha$
$CD^2=4^2+4^2-2\times 4\times 4\times\cos \alpha \Rightarrow CD^2=32(1-\cos \alpha )$
$\cfrac{CD}{\sin \alpha }=2r\Rightarrow r=\cfrac{CD}{2\sin \alpha } \Rightarrow r^2=\cfrac{CD^2}{4\sin^2 \alpha }=\cfrac{8(1-\cos \alpha )}{\sin^2\alpha }$
$\cfrac{AD}{4}=\tan (\cfrac{\pi}{2}-\alpha )=\cfrac{\sin(\cfrac{\pi}{2}-\alpha ) }{\cos(\cfrac{\pi}{2}-\alpha )}=\cfrac{1}{\tan \alpha} \Rightarrow \cfrac{AD}{2}=\cfrac{2}{\tan \alpha}$
$(\cfrac{AD}{2})^2=\cfrac{4}{\tan^2 \alpha},R^2=r^2+(\cfrac{AD}{2})^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{\sin^2 \alpha}=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}$
此时分子分母均为含$\cos \alpha$的两次项，先分离常数，变成分子为一次项，分母为二次项，再对分子整体换元。
$R^2=\cfrac{4\cos^2\alpha -8\cos \alpha +8}{1-\cos^2 \alpha}=-4+\cfrac{ -8\cos \alpha +12}{1-\cos^2 \alpha}=-4\cfrac{ 4(-2\cos \alpha +3)}{1-\cos^2 \alpha}$
$令 t=3-2\cos \alpha \in (1,3)\Rightarrow \cos^2 \alpha=\cfrac{1}{4}(3-t)^2,1- \cos^2 \alpha=-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}$
$R^2=f(t)=-4+\cfrac{4t}{-\cfrac{1}{4}t^2+\cfrac{6}{4}t- \cfrac{5}{4}}=-4+\cfrac{-16t}{t^2-6t+5}=-4+\cfrac{-16}{t-6+\cfrac{5}{t}}$
$t+\cfrac{5}{t}-6\ge 2\sqrt{5}-6\Rightarrow \cfrac{1}{t+\cfrac{5}{t}-6}\le \cfrac{1}{2\sqrt{5}-6}
\Rightarrow \cfrac{-16}{t+\cfrac{5}{t}-6}\ge \cfrac{-16}{2\sqrt{5}-6}=\cfrac{8}{3-\sqrt{5}}=6+2\sqrt{5}$
$\Rightarrow R^2=-4+6+2\sqrt{5}=2+2\sqrt{5},S=4\pi R^2=(8+8\sqrt{5})\pi$

10.棱长为2的正方体$ABCD-A_1B_1C_1D_1$中，P,Q分别是棱$CC_1,BC$的中点，动点M满足$\vec{DM}=\lambda \vec{DA} +\mu \vec{DD_1},其中\lambda ,\mu \in R$,则下列结论正确的是$(\qquad ABD)$
$A.若\lambda +\mu=1，则CM\perp DB_1;$
$B.若\lambda =\mu,则三棱锥B_1-AMC体积为定值;$
$C.若0\le\lambda\le 1 ,\mu=0.5,则直线PM与BC所成的角最小值为\cfrac{\pi}{3} ;$
$D.若动点M在三棱锥C-DPQ外接球上的表面上，则动点轨迹长度为\sqrt{2}\pi $
$解: A易证证。B选，M$为动点，不要以$M$所在的平面为底，要以$M$为棱锥的顶点。即三棱锥${\color{Red}M-ACB_1},M在对角线A_1D上，A_1D\parallel CB_1$
$C选，以D为坐标原点，DA,DC,DD_1为x,y,z轴建立坐标系，\overrightarrow{CB} =(2,0,0),\overrightarrow{PM}=(2\lambda ,-2,0)$
$\cos \alpha =\cfrac{\overrightarrow{CB}\cdot \overrightarrow{PM}}{|\overrightarrow{CB}|\times| \overrightarrow{PM}|}=\cfrac{\lambda }{\sqrt{\lambda ^2+1}}=\cfrac{1}{\sqrt{\cfrac{1}{\lambda ^2}+1}}\quad \lambda\in [0,1] \lambda=1时，\alpha=\cfrac{\pi}{4}$
$D.与上题一样，补全三棱锥{\color{Red} D-CPQ} $成三棱柱 ，动点M的轨迹为圆，即求圆的半径$r,PQ$为该圆的直径$,r=\cfrac{\sqrt{2}}{2},C=2\pi r= \sqrt{2}\pi$

11.如图，在一次社会实践中某学校数学探究实验组设计一个门把手，其 纵截面轮廓近似曲线$C：y^2=x^3-2x+2$的一部分，则$(\quad )$

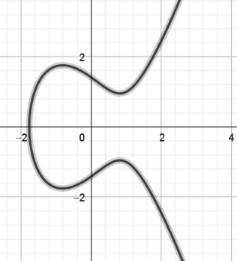
A.点(1,1)在C上；
B.在(1,1)处的切线，其与C的交点的横坐标均为整数；
C.若C在x 轴上方的部分为函数f(x)的图象，则$x=\cfrac{\sqrt{6}}{3}是f(x)$的最小值点；
D.C在y轴左边的部分到坐标 原点O的距离均大于$\sqrt{2}$.

13. 如图，$4\times 6$的方格纸(小正方形的边长为1)中有一个向量$\vec{OA}$(以图中的格点O为起点，格点A为终点),则满足
    $\vec{OA}\cdot \vec{OB}=1$的格点B共有多少个。
    
    14.设数列$\{a_n\}$的前n项和为$S_n,a_1=1,且2S_n=a_{n+1}-1(n\in N^*)$.若对于任意的正整数n,都有$a_1b_n+a_2b_{n-1}+a_3b_{n-2}+...+a_nb_1=3^n-n$成立。则满足等式$b_1+b_2+b_3+...+b_n=a_n$的所有正数数$n$的和为
    17.已知正项数列$\{a_n\}满足n\lg a_{n+1}=(n+1)\lg a_n且a_1=3$;
    $(1)求数列\{a_n\}的通项公式；$
    $(2)设b_n=\cfrac{a_n-1}{a_n+1},数列\{b_n\}的前n项和为S_n，求[S_{2025}]$

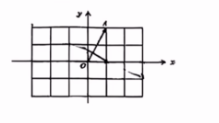
抛物线$y=x^2$上异于坐标原点$O$的两个不同的动点$A,B满足OA\perp OB.\triangle AOB$的面积是否存在最小值。若存在，请求出最小值；若不存在，请说明理由。
解：设$A(x_1,y_1)B(x_2,y_2)$直线AB的方程为$y=kx+m$,联立$\begin{cases} y=kx+m\\y=x^2\end{cases} \Rightarrow　x^2-kx-m=0$
$x_1+x_2=k,x_1x_2=-m\quad \overrightarrow{OA} \cdot \overrightarrow{OB}=x_1x_2+y_1y_2=0$
$y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=-k^2m+k^2m+m^2=m^2$
$\overrightarrow{OA} \cdot \overrightarrow{OB}=x_1x_2+y_1y_2=-m+m^2=0\Rightarrow m=1或m=0舍去$
$故直线l_{AB}过定点(0,1)，y=kx+1$
以直线的定点为界，将$\triangle AOB$分成左右两部分，故$S_{\triangle AOB}=\cfrac{1}{2}\times 1\times |x_1-x_2|=\cfrac{1}{2}\sqrt{k^2+4}\ge 1$

引申1.若直线$l与椭圆C:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)交于M,N$两点，A为椭圆的右顶点，且$AM\perp BN$.则直线$l过定点(\cfrac{e^2}{2-e^2}a,0)$
引申2.若直线$l与双曲线C:\cfrac{x^2}{a^2}－\cfrac{y^2}{b^2}=1(a\gt 0，b\gt 0)交于M,N$两点，A为双曲线的右顶点，且$AM\perp BN$.则直线$l过定点(\cfrac{e^2}{2-e^2}a,0)$
引申3.若直线$l与抛物线y^2=2px(p\gt 0)交于M,N$两点，A为抛物线顶点，且$AM\perp AN$.则直线$l过定点(2p,0)$

内准圆：$ A,B为椭圆/双曲线上两点， O为中心，且 OA\bot OB，过点 O作AB的垂线，垂足为H, |OH|为定值，$
$点H的轨迹为圆x^2+y^2=\cfrac{1}{\cfrac{1}{a^2}+\cfrac{1}{b^2}}=\cfrac{a^2b^2}{a^2+b^2},称为内准圆(PS:双曲线在离心率大于\sqrt{2}时才有内准圆)，AB是内准圆的切线$
$性质1:\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}=\cfrac{1}{a^2}+\cfrac{1}{b^2}$
$证明：设椭圆\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1,|OA|＝m,|OB|=n,A(m\cos \theta,m\sin \theta ),B(n\cos (\theta+\cfrac{\pi}{2}),n\sin(\theta+\cfrac{\pi}{2}))=(-n\sin \theta,n\cos \theta)$
$\cfrac{m^2\cos^2 \theta}{a^2}+\cfrac{m^2\sin^2 \theta }{b^2}=1\Rightarrow \cfrac{1}{m^2}=\cfrac{\cos^2 \theta}{a^2}+\cfrac{\sin^2 \theta }{b^2}$
$\cfrac{n^2\sin^2 \theta}{a^2}+\cfrac{n^2\cos^2 \theta }{b^2}=1\Rightarrow \cfrac{1}{n^2}=\cfrac{\sin^2 \theta}{a^2}+\cfrac{\cos^2 \theta }{b^2}$
$:\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}=\cfrac{1}{m^2}+\cfrac{1}{n^2}=\cfrac{1}{a^2}+\cfrac{1 }{b^2}\quad $
$性质2:垂足H的轨迹为 x^2+y^2=\cfrac{a^2b^2}{a^2+b^2}$
$证明(运用等面积代换),S_{\triangle OAB}=\cfrac{1}{2}|OA||OB|=\cfrac{1}{2}|AB||OH|\Rightarrow |OH|=\cfrac{|OA|OB|}{|AB|}$
$x^2+y^2=|OH|^2=\cfrac{|OA|^2|OB|^2}{|AB|^2}=\cfrac{|OA|^2|OB|^2}{|OA|^2+|OB|^2}=\cfrac{1}{\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}}=\cfrac{a^2b^2}{a^2+b^2}$即直角三角形直角边与斜边高的关系

例1、直线交椭圆$\cfrac{x^2}{4}+\cfrac{y^2}{3}=1于A、B，过原点作垂线交A,B于点P,|OP|=1$,是否存在直线$l使|AP||PB|=1$成立？若存在，求出$l$的方程；若不存在，请说明理由。
$解：由射影定理|AP||PB|＝|OP|^2，可知OA\perp OB,$然后用证明性质1的方法，证明$\cfrac{1}{OA^2}+\cfrac{1}{OB^2}=\cfrac{1}{a^2}+\cfrac{1}{b^2}=\cfrac{1}{4}+\cfrac{1}{3}=\cfrac{7}{12}$再用等面积法，得到直角三角形斜边上的高与两直角边的关系，得到$|OP|^2=\cfrac{a^2b^2}{a^2+b^2}=\cfrac{12}{7}$
这与$|OP|=1矛盾，所以不存在符合题意的直线l$

－－－

例2、2009年山东设椭圆$E:\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1(a\gt b\gt 0)过M(2,\sqrt{2}),N(\sqrt{6},1),Ｏ$为坐标原点。
①求E的方程；
②是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点$A、B,且OA\perp OB$?若存在，写出该圆的方程，并求$|AB|$的取值范围，若不存在，请说明理由。
解：①$\begin{cases} \cfrac{4}{a^2}+\cfrac{2}{b^2}=1\\ \cfrac{6}{a^2}+\cfrac{1}{b^2}=1\end{cases}\Rightarrow \begin{cases} \cfrac{x^2}{8}+\cfrac{y^2}{4}=1\end{cases}$
②设$|OA|=m,|OB|=n,|OA|的倾斜角为\theta，|OB|的倾斜角为\theta+\cfrac{\pi}{2}$
$A(m\cos \theta ,m\sin \theta),B[n\cos(\theta+\cfrac{\pi}{2}),n\sin (\theta+\cfrac{\pi}{2})]=(-n\sin \theta,n\cos \theta)$
$\begin{cases} \cfrac{(m\cos \theta)^2}{8}+\cfrac{(m\sin \theta)^2}{4}=1\\ \cfrac{(n\sin \theta)^2}{8}+\cfrac{(n\cos \theta)^2}{4}=1\end{cases}\Rightarrow \begin{cases} \cfrac{\cos^2 \theta}{8}+\cfrac{\sin^2 \theta}{4}=\cfrac{1}{m^2}=\cfrac{1}{|OA|^2}\\ \cfrac{\sin^2 \theta}{8}+\cfrac{\cos^2 \theta}{4}=\cfrac{1}{n^2}=\cfrac{1}{|OB|^2}\end{cases}$
$ \Rightarrow \cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}=\cfrac{1}{8}+\cfrac{1}{4}=\cfrac{3}{8}$
$Rt\triangle OAB,AB边为所求内准圆的切线，O到AB的垂足M(x,y)为所求的圆上的一点。$
容易得到$x^2+y^2=|OM|^2=\cfrac{|OA|^2|OB^2|}{|AB|^2}=\cfrac{1}{\cfrac{1}{OA^2}+\cfrac{1}{OB^2}}=\cfrac{8}{3}$
$|AB|^2=|OA|^2+OB^2|=(|OA|^2+|OB^2|)\cdot [\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}]\cdot\cfrac{8}{3}$
$=\cfrac{a^2b^2}{a^2+b^2}\cdot (\cfrac{OA^2}{OB^2}+\cfrac{OB^2}{OA^2}+2)$
$令t=\cfrac{OA^2}{OB^2},t\in [\cfrac{b^2}{a^2},\cfrac{a^2}{b^2}],即t\in[\cfrac{1}{2},2]$
$AB^2=f(t)=\cfrac{a^2b^2}{a^2+b^2}\cdot (t+\cfrac{1}{t}+2)\quad $由对勾函数性质可知，$t=1时f(t)$取得最小值$f(t)=\cfrac{8}{3}\times 4=\cfrac{32}{3};t=\cfrac{1}{2}或2时，f(t)$取得最大值,$f(t)=\cfrac{8}{3}\times \cfrac{9}{2}=12$
$故|AB|取值范围[\cfrac{4}{3}\sqrt{6},2\sqrt{3}]$

$双曲线的内准圆设M,N在双曲线\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1(b\gt a\gt 0)上，且有OM\perp ON，则：$
$①圆x^2+y^2=\cfrac{a^2b^2}{b^2-a^2}与直线MN相切，这里的圆称为双曲线的内准圆$
$②\cfrac{1}{|OM|^2}+\cfrac{1}{|ON|^2}=\cfrac{1}{a^2}-\cfrac{1}{b^2}为定值。$

双曲线的外准圆设双曲线$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1(a\gt b\gt 0)外有一点P$，过点$P$的双曲线的两条切线相互垂直，则$P的轨迹是圆x^2+y^2=a^2-b^2$,这里的圆称为双曲线的外准圆，或者蒙日圆。